Neural Network to Matrix

Basics

For a set of basis functions \(B=\{\Phi_1, \Phi_2\}\) in \(R^3\) any vector \(v\) in the plane spanned by the basis is expressed by linear combination of the basis functions.

\[\begin{align*} v &= c_1\Phi_1 + c_2\Phi_2 \\ v &= \begin{bmatrix}\Phi_1 & \Phi_2\end{bmatrix} \begin{bmatrix}c_1 \\ c_2\end{bmatrix} \\ v &= \begin{bmatrix}\phi_{11} & \phi_{12} \\ \phi_{21} & \phi_{22} \\ \phi_{31} & \phi_{32}\end{bmatrix} \begin{bmatrix}c_1 \\ c_2\end{bmatrix} \\ v & = \Phi C \end{align*}\]

The projections of \(v\) on the basis functions are given by the dot product of \(v\) with \(\Phi\).

\[\begin{align*} p_1 &= \Phi_1^T v \\ p_2 &= \Phi_2^T v \\ \begin{bmatrix}p_1 \\ p_2\end{bmatrix} &= \Phi^T v \end{align*}\]

A few things to be noted here.

• We can think of getting \(v\) from coordinate \(C\) as a LINEAR transformation or mapping by matrix \(\Phi\) operating on \(C\). 2D input \(C\) is mapped to 3D output \(v\).
• In matrix \(\Phi\) columns are composed of the basis functions.
• \(\Phi\) needs as many columns or bases as dimension of input \(C\). This should be the case not only for matrix multiplication but also for linear combination of basis functions as one would need as many \(c_i\) as basis functions.
• A vector has the dimension of the space it resides in. For output in this case dimension is \(R^3 \to 3\). Dimension is the number of items needed in a vector to fully represent it.
• \(\phi_{ij}\) means it is i-th component of \(\Phi_j\).

Neural Network

Lets consider a layer of neural network. Input is \(X = [x_1, x_2, \cdots, x_u]^T\) and through a linear transformation \(W\) we get output \(N=[n_1, n_2, \cdots, n_v]^T\).

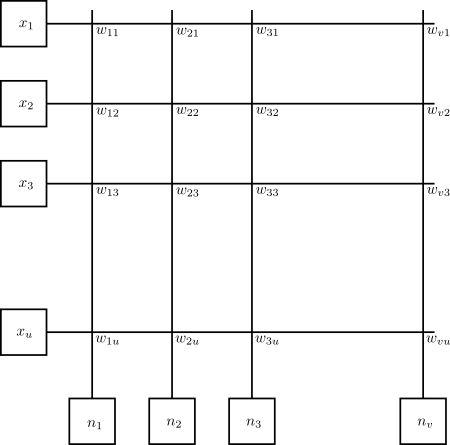
\[N = WX\]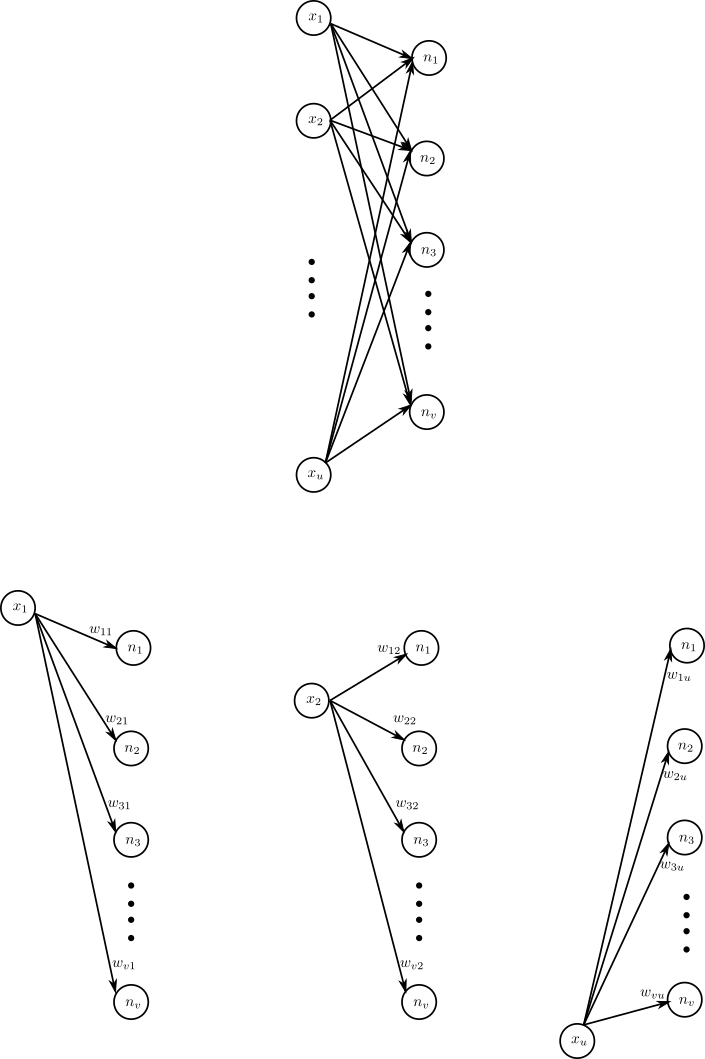

The output of the layer (before any nonlinearity is applied) is linear combination of the weights. Using the notes from the basics we can easily construct the transfromation matrix for the neural network.

• Output needs \(v\) elements. Hence, output is \(v\) dimensional.
• Input needs \(u\) elements. Hence, input is \(u\) dimensional.
• Matrix \(W\) needs \(u\) number of column vectors, each column for each input element. Each column will consist of \(v\) elements.
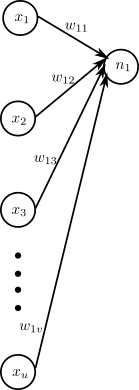
• The columns of \(W\) consists of weights of each output neuron’s weight associated with an element of input. The full transformation looks as follows.

\[\begin{align*} N &= x_1W_1 + x_2W_2 + \cdots + x_uW_u \\ N &= \begin{bmatrix}W_1 & W_2 & \cdots & W_u\end{bmatrix}X \\ \begin{bmatrix}n_1\\n_2\\ \vdots \\ n_v\end{bmatrix} &= \begin{bmatrix}w_{11} & w_{12} & \cdots & w_{1u} \\ w_{21} & w_{22} & \cdots & w_{2u} \\ \vdots & \vdots & \ddots & \vdots \\ w_{v1} & w_{v2} & \cdots & w_{vu} \end{bmatrix} \begin{bmatrix}x_1\\x_2\\ \vdots \\ x_u\end{bmatrix} \end{align*}\]

• The rows of matrix \(W\) forms the filter for each neuron. The i-th row forms filter for i-th neuron. We can think of each output of the neuron as dot product of corresponding rows of \(W\) and \(X\).

\[n_i = \begin{bmatrix}w_{i1} & w_{i2} & \cdots & w_{iu}\end{bmatrix}X\]

• \(w_{ij}\) means it is the weight of i-th neuron for j-th input \(x_j\)

Vector Matrix Multiplier

With the above formalism, the weights can be easily transfered to a Vector Matrix Multiplier (VMM). For the VMM as shown in figure below, the input padas are on the left and outout pads are at the bottom. Here each column of matrix \(W\) runs horizontaly. Hence, transposing \(W\) would be required to map the weights to VMM.