Order From Chaos

I was quite taken aback when I saw it for the first time. How can the randomness of any activity can lead to strikingly ordered outcome? The reality that we see and experience, is it as precisely structrued as we think it is? Although later as spent some time on it, it became clear that randomness has little to do with the outcome. Rather there was a profound revealation that very a complex outcome has a very simple prosess.

Lets imagine we have three points on a plane that are fixed. There is another point randomly placed in that plane. That piont can move with a rule. It can randomly move towards one of those fixed points halfway of the distance between them. And this process repeates. If the moving point leaves marks everywhere it goes then what do you think you will observe after a long enough time of repeating the process?

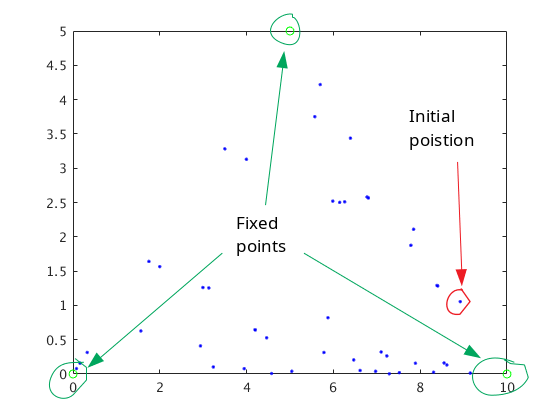
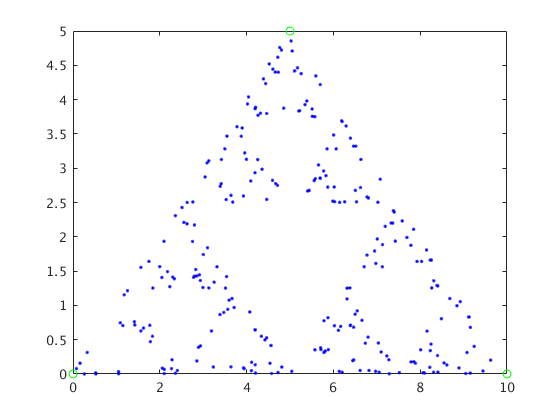
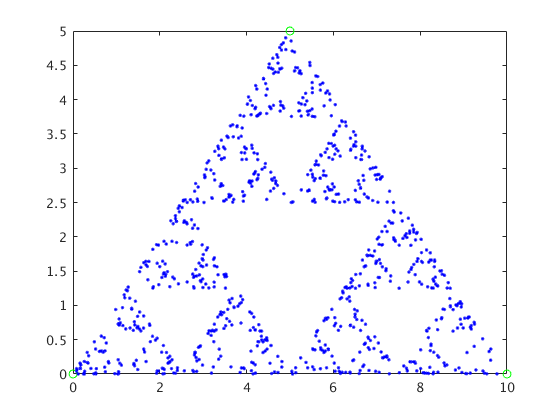
At first it looks like it is totally random. But after some repeatition a shape begin to emerge! At first we might predict that the shape is going to be traingle because the moving point is only moving towards three points. But shape that emerges is not as simple as a triangle. The final shape that emerges is a fractal, self repeating structure know as Sierpinski Triagle. This is an unexpected result. Because it was not expected to produce something like this out of random motion.

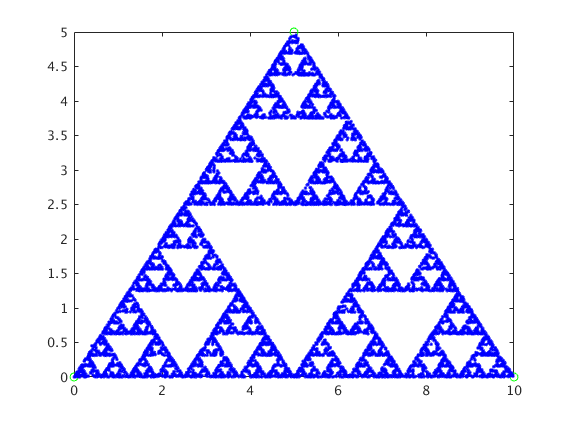
What is most striking to me is that something as complex as this structure can be encoded in a very simple set of rules. This is important to me because I am looking for a way to encode information in Neural Networks. Could this be the one of the ways that our brain is storing information? May be. I have to find that out. The follwing MATLAB code generates the images above. Later I figured that randomness has nothing to do with the shape. As long as the point moves on the rule of moving halfway towards the fixed points, this shape will appear. Randomness of selecting which direction to go just ensures that all the direction is covered. We could this by splitting the initial point into three points and go towards all the three points. And the resulating points would split into three points each and repeat the process. But this way number of points increases exponentially and becomes hard on memory. Randomness is a way to avoid that. Pretty impressive.

% three point
p1 = [0;0]; p2 = [10;0]; p3=[5;5];
p = [p1, p2, p3]; % or generate three random points % p = rand(2,3)*10;
x = p(1,:); y = p(2,:);
plot(x,y, 'go');

% do random playing
seed_p = rand(2,1);
MAX_P = length(p);
MAX_itr = 10^4;
for i = 1:MAX_itr
    r = randperm(MAX_P, 1);
    f = 1/2;
    next_p = seed_p + f*(p(:,r)-seed_p);
    hold on; pause(0.010);
    plot(next_p(1,:), next_p(2,:),'b.');
    seed_p = next_p;
end

This amazed me without a doubt. But I was not ready for what came next. The following image is known as Barnsley Fern which was generated by computer following similar set of rules placing points randomly. I will code it up and post the codes here someother day.