Statistical Approach To Find The Value Of \(\pi\)

\(\pi\) is something very sacred to mathematics and engineering. It is alos one of those divine values that binds the very existance of our universe. One way \(\pi\) is interesting is that it is not a ratioed number. It cannot be expressed in terms of fraction of two whole numbers. The digits after the decimal will never end. Yet it is a finite number. There a very straight forward way to measure the value of \(\pi\). It is defined to be the ratio of the perimeter and radius of a circle. We can make a circle out of a cardboard. Take a measuring tape and measure the perimeter and radius. Take the ratio and there you have it. If you are feeling rather bored you can take the Leibniz formula to calculate \(\pi\) as given below. \begin{equation} \frac{\pi}{4} = 1 - \frac{1}{3} + \frac{1}{5} - \frac{1}{7} + \frac{1}{9} - \cdots \nonumber \end{equation} But there are some ‘fun to experiemtn with’ approach to calculate \(\pi\). One of them is to use statistics. Before we do that lets build our theory. There is a square and there is a circle which fits inside the square. Lets assuem the sqare has sides of length \(x\). Incidentally the diameter of the cirle is also \(x\). The area of the square (\(A_s\)) and the circle (\(A_c\)) is

\[\begin{eqnarray} A_s &= x^2 \nonumber \\ A_c &= \pi\frac{x^2}{4} \nonumber \end{eqnarray}\]

If we take the ratio of the aerea of the circle and the square we get the value of \(\pi\) divided by 4. So if we multipliy the ratio with 4 we will end up with \(\pi\).

\[\begin{eqnarray} \frac{A_c}{A_s} = \frac{\pi}{4} \nonumber \end{eqnarray}\]

If can figure out the area of circle and the square we can also figure out the value of \(\pi\). Now back to statistical approach. If we spread some particles uniformly over the square containing the circle number of particles on the square will be propotional to the area of the sqaure. Similarly number of particles on the circle will be propotional to the area of the circle. Hence we can approximate the area of the circle and square by counting the number of particles on them.

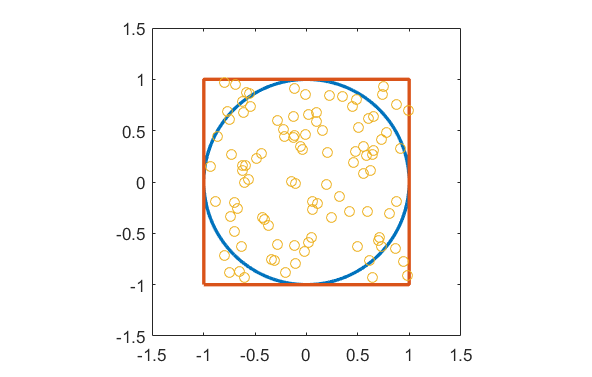
But to get colse to accurate results we need as many particles as possible. This will be tiresome do by hand. We will use a computer to do that. I am using MATLAB. A group of coordinates for the particles can be generated with rand() function to be within [-1 1]. [-1 1] is because I will be using a circle of radius 1. Which means the square will be of length 2. The span [-1 1] has lenght of the side of the square. Then we can calculate how many particles are inside the circle. In other words how many of the particles has distance less than 1 from the origin. The we can simply find out the fraction.

% calculate pi
n = 1e6;
coord = rand(n,2) - 0.5;
coord = 2*coord;
x = coord(:,1);
y = coord(:,2);
isInside = (x.^2 + y.^2) < 1;
fraction = sum(isInside)/n;
fraction*4

rand() function produces random number within [0 1]. So 0.5 is subtracted to produce numbers inside [-0.5 0.5]. Then it is mumtiplied with 2 to produces number in [-1 1]. A particle number of one million produces fairly accurate result. This table show how the accuracy varies with number of total particles.

Table : Accuracy of \(\pi\)

n	fraction*4
1e2	3.0400
1e3	3.2120
1e4	3.1620
1e5	3.1417
1e6	3.1423

Code for generating the plot above.

% draw square and circle
theta = 0:0.001:2*pi;
r = 1; % circle radius
xC = r*cos(theta);
yC = r*sin(theta);
figure, plot(xC, yC, 'LineWidth', 2);
axis equal;
a = 2; % square side
xs = -1; ys = -1;
xS = [xs xs xs+a xs+a xs];
yS = [ys ys+a ys+a ys ys];
hold on;  plot(xS, yS, 'LineWidth', 2);
xlim([-1.5 1.5]); ylim([-1.5 1.5]);
% spread some particles;
n = 1e2;
coord = rand(n,2) - 0.5;
coord = 2*coord;
x = coord(:,1);
y = coord(:,2);
hold on; plot(x,y,'o');